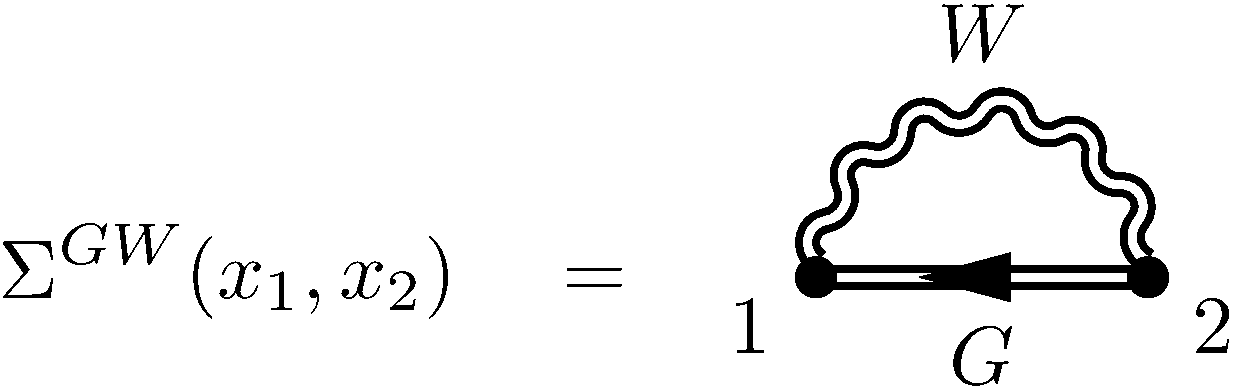The GW approximation
 The band gap is a fundamental quantity for a solid, like the HOMO-LUMO gap for an atom or a molecule.
They are both defined as the difference $E_g = E_\mathrm{IP} - E_\mathrm{EA}$ between the ionization potential,
that is the energy to be provided to remove an electron from the system,
and the electron affinity, that is the energy released when adding an electron to the system.
The electronic structure of a solid is characterized by the band gap and more in general by the band plot,
both can be measured in photoemission experiments.
The band gap is a fundamental quantity for a solid, like the HOMO-LUMO gap for an atom or a molecule.
They are both defined as the difference $E_g = E_\mathrm{IP} - E_\mathrm{EA}$ between the ionization potential,
that is the energy to be provided to remove an electron from the system,
and the electron affinity, that is the energy released when adding an electron to the system.
The electronic structure of a solid is characterized by the band gap and more in general by the band plot,
both can be measured in photoemission experiments.
From the theory point of view, the quasiparticle energy of an excitation corresponds
to the energy required to remove/add an electron from/to a many-particle system.
It is the solution of a non-linear and energy-dependent equation, the quasiparticle equation, in which all
the many-body interaction effects among the electrons of the system, are accounted by
the self-energy.
The GW approximation
is the first-order perturbative expansion of the electronic self-energy
in terms of the screened interaction $W$.
In the GW approximation vertex corrections are neglected and
the self-energy reduces to a simple direct product (in real space)
of the Green function or dressed electron propagator $G$ and the
dynamically screened interaction $W$, $\Sigma^{GW} = i G(x_1,x_2) W(x_1^+,x_2)$,
or diagrammatically:
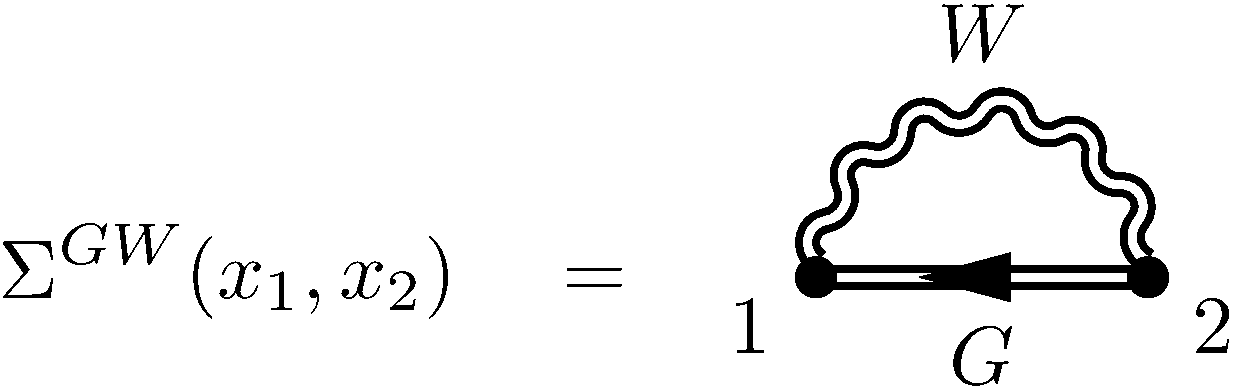
The first GW calculation on the jellium model is due to Hedin 1965.
First ab initio calculations in real systems are due to
Strinati, Mattausch and Hanke 1980
and 1982
( $G_0W_0$ on top of Hartree-Fock, HF)
and then to
Hybertsen and Louie 1985, and
Godby, Schlüter and Sham 1987
( $G_0W_0$ on top of density-functional theory in the local-density approximation, DFT-LDA).
They all showed that already a non-self-consistent
G0 W0 self-energy always improves the band gap toward the experiment,
reducing the HF and increasing the DFT-LDA band-gaps,
achieving an error of around 1% with respect to angle-resolved
photoemission (ARPES) experiments.
Since then, the validity of the GW approximation has been confirmed by many
other calculations.
Here a figure reporting a statistics over several G0 W0 calculations of the band gap in literature,
starting with the statistics reported in the 1999 Hedin review.
Disclaimer: The authorship for the informations hereby provided belongs to Valerio Olevano who assumes full liability and responsability.